Méthode d'assimilation - 4DVar
Par jOas le vendredi, novembre 16 2007, 00:14 - Assimilation - Lien permanent
Le 4D-Var est l'extension temporelle du 3D-Var. Cette méthode ne vise pas à obtenir l'état optimal à un instant donné, mais la trajectoire optimale sur une fenêtre de temps donné. Les observations sont donc prises en compte aussi bien dans leur distribution spatiale que temporelle. Cet aspect est déjà pris en compte par le 3D-Var FGAT présenté dans la section ad-hoc. Néanmoins, le 4D-Var apporte un aspect temporel en plus car il propage l'information apportée par les observations à l'instant initial de la fenêtre d'assimilation. De ce fait, l'analyse obtenue doit permettre au modèle d'évolution d'avoir la trajectoire la plus proche possible de l'ensemble des observations utilisées.
Cette amélioration du 3D-Var permet d'ajouter la connaissance de l'évolution du système comme information pour l'analyse.
De nombreuses applications à des modèles réalistes météorologiques (Thépaut et Courtier, 1991 et Zupanski, 1993) et océanographiques (Moore, 1986 ; Shröter etal., 1993 ; Luong etal., 1998 et Greiner etal., 1998) ont depuis longtemps été effectuées.
L'amélioration ainsi apportée, conjuguée au fort développement des moyens de calculs, font que le 4D-Var est venu remplacer le 3D-Var dans les systèmes de prévision opérationnels atmosphériques du CEPMMT en 1997 et de Météo-France en 2000.
4D-Var classique
Soit \[M_{0 \to i}\] l'opérateur a priori non-linéaire qui permet de propager l'état du système \[\mathbf{x}\] de \[t_0\] à \[t_i\] :
\[ \forall i, \qquad \mathbf{x}(t_i) = M_{0 \to i}(\mathbf{x})\].
En supposant, dans un premier temps, le modèle parfait, la fonction coût \[J\] du 4D-Var se décompose, comme pour le 3D-Var, en un terme \[J^b\] lié à l'ébauche et un autre \[J^o\] lié aux observations.
En tenant compte des instants de mesures \[t_i\], la matrice de covariance d'erreur des observation est notée \[\mathbf{R}_i\] et l'opérateur d'observation non-linéaire \[H_i\]. Les observations \[\mathbf{y}^o_i\] sont donc comparées à leur équivalent modèle \[H_i\mathbf{x}(t_i)\] à chaque instant d'observation. Le calcul du terme \[J^o\] nécessite l'intégration du modèle d'évolution de \[t_0\] à \[t_N\]. Le vecteur d'état \[\mathbf{x}\] est ainsi propagé par le modèle numérique \[M_{0 \to N}\] de \[t_0\] à \[t_N\] où \[N\] représentent le nombre de pas de temps de l'intégration du modèle à l'intérieur d'un cycle d'assimilation.
L'algorithme d'assimilation identifie un état \[\mathbf{x}^a\] de la variable \[\mathbf{x}\] à l'instant \[t_0\] (une condition initiale), qui, intégré par le modèle d'évolution fournit une trajectoire optimale au sens des moindres carrés (la trajectoire analysée) sur l'ensemble de la fenêtre d'assimilation (Les vecteurs \[\mathbf{x}^a(t_0)\] et \[\mathbf{x}^b(t_0)\] sont notés \[\mathbf{x}^a\] et \[\mathbf{x}^b\]. \`A tout autre moment que l'instant initial \[t_0\], les notations \[\mathbf{x}^a(t_i)\] et \[\mathbf{x}^b(t_i)\] seront utilisées.) :
\[ J^o(\mathbf{x}) = \frac{1}{2}\sum_{i=0}^N \left(\mathbf{y}^o_i - H_i\mathbf{x}(t_i)\right)^T\mathbf{R}_i^{-1} \left(\mathbf{y}^o_i - H_i\mathbf{x}(t_i)\right)\],
\[J^o(\mathbf{x}) = \frac{1}{2}\sum_{i=0}^N \left(\mathbf{y}^o_i - H_i M_{0\to i}(\mathbf{x})\right)^T\mathbf{R}_i^{-1} \left(\mathbf{y}^o_i - H_i M_{0\to i}(\mathbf{x})\right)\],
où \[G_i\mathbf{x}=H_i\mathbf{x}(t_i)=H_i M_{0\to i}(\mathbf{x})\]. L'opérateur \[G_i\] est appelé l'opérateur d'observation généralisé pour l'état \[\mathbf{x}\] propagé par le modèle de \[t_0\] à \[t_i\].
L'état optimal \[\mathbf{x}^a\], qui minimise la fonction coût \[J\], est obtenu quand le gradient de cette fonctionnelle est nul. Comme pour le 3D-Var, ce gradient s'obtient simplement :
Les opérateurs \[\mathbf{H}_i\], \[\mathbf{M}_{0\to i}\] et \[\mathbf{G}_i=\mathbf{H}_i \mathbf{M}_{0\to i}\] sont les opérateurs linéarisés de \[H_i\], \[M_{0\to i}\] et \[G_i\] au voisinage de l'ébauche. L'opérateur \[\mathbf{M}^T_{0\to i}\] est l'adjoint de l'opérateur linéarisé \[\mathbf{M}_{0\to i}\].
Équivalence avec le filtre de Kalman
Si les opérateurs \[H\] et \[M\] sont linéaires, alors la fonction coût \[J\] est quadratique. Si de plus le modèle est parfait (hypothèse émise dans la section précédente), alors la solution du 4D-Var à la fin de la fenêtre d'assimilation est identique à celle du filtre de Kalman (Jazwinski, 1970 ; Ghil etal., 1981 et Lorenc, 1986). En météorologie comme en océanographie, \[H\] et \[M\] sont souvent faiblement non-linéaires. Dans ce cas, la minimisation peut être effectuée avec un algorithme adapté aux fonctions coûts non-quadratiques. Généralement, l'opérateur généralisé d'observation linéarisé \[\mathbf{H}_i\] et le modèle linéaire-tangent \[\mathbf{M}_{0\to i}\] sont supposés de bonnes approximations de \[H_i\] et \[M_{0\to i}\] sur la fenêtre temporelle d'assimilation. La validité du linéaire-tangent dépend d'une part de la formulation du modèle numérique et de l'opérateur d'observation considérés mais aussi du contexte de l'assimilation, notamment la durée de la fenêtre d'assimilation, de la physique des phénomènes représentés et de la région d'étude.
Calcul de la fonction coût et de son gradient
Le terme d'ébauche de la fonction coût \[J^b\] est identique à celui décrit pour le 3D-Var. Son évaluation est directe pour tout état de la variable d'état \[\mathbf{x}\]. L'évaluation du terme lié aux observations \[J^o\] est, par contre, plus ardue. Dans le cadre du 3D-Var, \[J^o\] est une combinaison linéaire des écarts entre les observations et l'état du modèle à un instant donné. \`A présent, chaque évaluation de \[J^o\] requiert l'intégration du modèle sur la fenêtre d'assimilation.
L'équation \[\nabla J=0\] ne peut être résolue directement. Une solution minimisant la fonction coût \[J\] par une méthode de descente itérative utilisant la valeur de \[\nabla J\] est envisageable. Généralement, l'état d'ébauche \[\mathbf{x}^b\] est utilisé comme une première estimation de l'état analysé. Le gradient de la fonction coût \[\nabla J\] peut être estimé de manière très efficace par la méthode adjointe (Une description complète des méthodes adjointes est présentée dans Thacket et Long (1988). En fait, l'évaluation du terme \[\nabla J^o\] peut se résumer à une intégration du modèle direct et une intégration du modèle adjoint (Le Dimet et Talagrand, 1986). Le gradient de la fonction coût est évalué par rapport à \[\mathbf{x}\] décrivant le vecteur d'état à l'instant initial de la fenêtre d'assimilation
où \[\mathbf{x}^*\] représente l'adjoint de la variable \[\mathbf{x}\].
La méthode adjointe permet une évaluation efficace du gradient de la fonction coût dans l'algorithme du 4D-Var. Néanmoins, cette opération implique qu'une version adjointe du modèle d'évolution linéarisé soit disponible. Cette contrainte est souvent l'étape cruciale à surmonter lors de l'implémentation de l'algorithme d'assimilation 4D-Var. En effet, dans de nombreux domaines, comme la météorologie et l'océanographie, les modèles d'évolution sont souvent complexes et non-linéaires. Deux étapes sont généralement nécessaire : écrire le modèle linéaire-tangent du modèle d'évolution ; puis écrire son adjoint. Ces opérations peuvent être effectuées soit manuellement, soit par des méthodes de linéarisation et d'adjoint automatiques (Giering et Kaminski, 1998). Malheureusement, ces méthodes automatiques ne sont pas capables de présumer les hypothèses de linéarisation qui sont faites manuellement et les modèles linéaire-tangent et adjoint obtenus sont souvent très coûteux. Néanmoins, l'utilisation conjointe d'une méthode automatique et d'une écriture manuelle permet d'obtenir assez rapidement des modèles tangent-linéaire et adjoint efficaces.
Coût de calcul du 4D-Var
L'intégration du modèle direct pour le calcul des innovations, puis pour la propagation de l'analyse, ainsi que l'intégration du modèle adjoint font du 4D-Var une méthode très coûteuse. Elle est néanmoins applicable en météorologie et, dans une moindre mesure, en océanographie. En effet, la plupart des grands centres opérationnels de météorologie utilisent des méthodes 4D-Var. Néanmoins, à la différence des centres océanographiques, leur capacité de calcul est très importante. Ainsi, le 4D-Var a été utilisé dans de nombreuses études en océanographie, notamment pour assimiler des données altimétriques dans des modèles régionaux quasi-géostrophiques (Moore, 1991), dans des modèles à gravité réduite (Weaver et Anderson, 1997), dans des modèles "shallow-water" (Greiner et Périgaud, 1994), dans des modèles aux équations primitives (Stammer etal., 1997 ; Greiner etal., 1998a, b) et dans des modèles couplés (Lee etal., 2000).
Le 4D-Var à contrainte faible
Dans la présentation du 4D-Var, le modèle a été considéré comme parfait. C'est-à-dire que le modèle décrivait exactement le comportement du système. Dans ce cas, le 4D-Var est décrit comme à contrainte forte (Sasaki, 1970). Cependant, malgré l'utilisation de modèles extrêmement sophistiqués, ceux-ci comportent des erreurs qui ne peuvent être négligées et qui ne pourront jamais l'être pour des systèmes aussi complexes que l'atmosphère ou l'océanographie.
Comme pour le filtre de Kalman, l'ajout d'un terme correctif directement dans la fonction coût est possible. En définissant l'erreur du modèle telle que
la fonction coût \[J\] peut alors s'écrire
\[+\frac{1}{2}\sum_{i=0}^N \left(\mathbf{y}^o_i-G_i\mathbf{x}\right)^T\mathbf{R}_i^{-1} \left(\mathbf{y}^o_i-G_i\mathbf{x}\right)\]
\[+\frac{1}{2}\sum_{i=0}^N\mathbf{q}_i^T\mathbf{Q}_i^{-1}\mathbf{q}_i\],
où \[\mathbf{Q}_i\] est la matrice de covariance d'erreur modèle à l'instant \[t_i\].
Cette formulation du 4D-Var est dite à contrainte faible et il est nécessaire de proposer une modélisation de la matrice de covariance d'erreur modèle \[\mathbf{Q}\]. De nombreux travaux par Derber (1989), Stammer etal. (1997), Bennet etal. (1998), Lee et Marotzke (1998) ou Vidard (2001) utilisent cette algorithme du 4D-Var à contrainte faible.
Évolution temporelle de la matrice de covariance d'erreur d'ébauche
L'impact de la prise en compte du caractère temporel est clairement mis en évidence dans la fonction coût liée aux observations \[J^o\]. Cependant, l'aspect temporel de la matrice de covariance d'erreur d'ébauche \[\mathbf{B}\] est moins évident dans un premier temps. En effet, la dynamique du modèle d'évolution est prise en compte implicitement par la matrice de covariance d'erreur d'ébauche \[\mathbf{B}\] sur chaque fenêtre d'assimilation, et donc dans la fonction coût liée à l'ébauche \[J^b\].
L'erreur d'ébauche à l'instant \[t_0\] est l'écart entre l'ébauche et l'état vrai au début de la fenêtre d'assimilation \[{\epsilon}^b=\mathbf{x}^b-\mathbf{x}^t\]. \`A tout instant \[t_i\] du cycle d'assimilation, cette erreur notée \[{\epsilon}^b(t_i)\], est l'écart entre l'état vrai \[\mathbf{x}^t(t_i)\] et l'ébauche \[\mathbf{x}^b(t_i)\] sous l'hypothèse que le modèle est linéaire :
\[{\epsilon}^b (t_i)=M_{0\to i}\mathbf{x}^b - M_{0\to i}\mathbf{x}^t\]
\[{\epsilon}^b(t_i)\approx\mathbf{M}_{0\to i}\left(\mathbf{x}^b-\mathbf{x}^t\right)\]
\[{\epsilon}^b(t_i)\approx\mathbf{M}_{0\to i}{\epsilon}^b\].
La matrice de covariance d'erreur à l'instant \[t_i\] est alors donnée par
\[ E\left[{\epsilon}^b(t_i)({\epsilon}^b(t_i))^T\right]=\mathbf{M}_{0\to i}\mathbf{B}\mathbf{M}_{0\to i}^T\].
Cette matrice décrit les erreurs liées à l'ébauche aux instants d'observations. La matrice de covariance d'erreur d'ébauche \[\mathbf{B}\] est donc implicitement propagée en temps par le 4D-Var à travers la dynamique du modèle linéaire-tangent \[\mathbf{M}_{0\to i}\] et son adjoint \[\mathbf{M}_{0\to i}^T\]. Le 4D-Var présente donc une analyse cohérente avec la dynamique du système (Thépaut etal., 1993).
Équivalence avec le 3D-Var FGAT
Il existe une similarité frappante entre le 3D-Var FGAT (Eqs. (048a} et (048b}) et le 4D-Var à contrainte forte (Eqs. (051} et (052}). En effet, il suffit de définir le modèle d'évolution dans le 4D-Var comme l'identité (\[M=\mathbf{I}\]), pour que le l'opérateur généralisé d'observation \[G\] se réduise à l'opérateur d'observation non-linéaire \[H\] et que le 4D-Var à contrainte forte devienne un 3D-Var FGAT.
C'est une caractéristique très intéressante car elle permet très facilement, du point de vue de l'implémentation informatique, de passer d'une méthode à l'autre. Étant donné le coût informatique du 4D-Var, cette approche permet une évolution simple et naturelle du 3D-Var FGAT vers le 4D-Var en fonction de l'évolution des capacités informatiques disponibles.
Formulation incrémentale du 4D-Var
La formulation incrémentale a déjà été abordée rapidement à propos du 3D-Var dans la section ad-hoc, mais elle prend avec le 4D-Var tout son sens.
En effet, l'introduction de l'approche incrémentale en météorologie a été motivée par la réduction de coût qu'elle propose. Dans le cadre du 4D-Var classique décrit précédemment, à chaque itération de la minimisation de la fonction coût (Eqs. (051} et (052}), l'intégration du modèle direct non-linéaire et de l'adjoint du modèle linéarisé est très coûteuse. Les non-linéarités des modèles numériques atmosphériques peuvent conduire à des fonctions coûts complexes. Les minimiseurs utilisés sur ces fonctions n'aboutissent pas forcément à une minimisation fiable et ce, de surcroît, à un coût élevé. Ces non-linéarités compliquent de plus, lourdement la tâche de l'écriture de l'adjoint (Xu, 1996). Dans l'approche incrémentale, la fonction coût est rendue quadratique, ce qui garantit l'identification d'un minimum unique par une méthode de descente pour un coût de calcul notablement inférieur à celui du problème non-linéaire. Le modèle linéaire-tangent est écrit avec une physique simplifiée, ce qui facilite grandement l'écriture de l'adjoint du modèle. De plus, une approche communément choisie en météorologie est d'utiliser un modèle linéaire-tangent à une résolution plus basse que celle du modèle non-linéaire. Le coût de la minimisation du 4D-Var en est significativement réduit. C'est formulation incrémentale de l'approche variationnelle du 4D-Var qui a permis de le rendre applicable de façon opérationnelle pour la prévision météorologique (Courtier etal., 1994 et Rabier etal., 2000).
Dans la formulation incrémentale de l'assimilation variationnelle, l'objectif est de minimiser la fonction coût, non plus par rapport à la variable d'état \[\mathbf{x}\], mais par rapport à un incrément \[\delta\mathbf{x}\] tel que \[\mathbf{x}=\mathbf{x}^b+\delta\mathbf{x}\]. L'hypothèse principale de la formulation incrémentale est d'utiliser un modèle d'évolution et un opérateur d'observation linéarisé pour propager l'incrément mais de conserver le modèle non-linéaire pour la propagation de l'ébauche \[\mathbf{x}^b\]. La solution de la minimisation est l'incrément d'analyse \[\delta\mathbf{x}^a\] à \[t_0\] tel que le vecteur d'analyse \[\mathbf{x}^a\] soit
En supposant que l'ébauche \[\mathbf{x}^b\] est une "bonne" approximation a priori de l'état optimal du système au sens des moindres carrés, l'incrément \[\delta\mathbf{x}\] devrait être petit. Les opérateurs non-linéaires d'observation \[H\] et du modèle \[M\] sont linéarisés au voisinage de l'ébauche de sorte que pour tout état du modèle \[\mathbf{x}\], à chaque instant \[t_i\] de la fenêtre temporelle d'assimilation,
\[ \mathbf{x}(t_{i+1})=M_{0\to i}\mathbf{x}\] \[ \mathbf{x}(t_{i+1})=M_{0\to i}(\mathbf{x}^b+\delta\mathbf{x})\]
Par conséquent
où \[\mathbf{M}_{0\to i}\], \[\mathbf{H}_i\] et \[\mathbf{G}_i\] sont les opérateurs linéarisés à \[t_0\] autour de l'ébauche \[x^b\] de \[M_{0\to i}\], \[H_i\] et \[G_i\].
\[ \mathbf{M}_{0\to i}=\left.\frac{\partial M_{0\to i}}{\partial \mathbf{x}}\right|_{\mathbf{x}=\mathbf{x}^b} \],
\[ \mathbf{H}_i=\left.\frac{\partial H_i}{\partial \mathbf{x}}\right|_{\mathbf{x}=\mathbf{x}^b} \],
En insérant les Eqs. (060}, (061} et (062} dans la formulation de la fonction coût donnée par les Eqs. (051} et (052}, elle peut être reformulée de manière incrémentale
où \[\mathbf{d}_i=\mathbf{y}^o_i-G_i\mathbf{x}^b=\mathbf{y}^o_i-H_i\mathbf{x}^b(t_i)\] représente l'innovation au temps \[t_i\], c'est-à-dire l'écart entre les observations et l'équivalent de l'ébauche donné par l'opérateur d'observation généralisé \[G_i\] dans l'espace des observations à chaque temps \[t_i\].
La fonction coût \[J=J^b+J^o\] du 4D-Var incrémental à contrainte forte est quadratique et la minimisation possède une solution unique. Si la linéarisation des opérateurs \[H_i\], \[M_{0\to i}\] et \[G_i\] est exacte, alors la solution est identique à celle obtenue par le filtre de Kalman étendu.
L'incrément d'analyse qui minimise la fonction coût donné par les Eqs. (064} et (065} est
La fonction coût incrémentale (Eqs. (064} et (065}) est minimisée par une méthode itérative de descente. Cette minimisation nécessite le calcul de la fonction coût et de son gradient à chaque itération de la minimisation comme pour l'algorithme classique du 4D-Var. Avant le début de la minimisation, l'état d'ébauche à \[t_0\] noté \[\mathbf{x}^b\] est propagé par le modèle non-linéaire permettant le calcul des innovations \[\mathbf{d}_i\] à chaque instant d'observation \[t_i\].
La figure 4DVar permet de représenter simplement l'utilisation du 4D-Var incrémental. Elle est à comparer aux Figs. 3DVar3 et 3DVar4 qui représentent, selon les mêmes codes, les 3D-Var FGAT incrémental avec ou sans IAU.
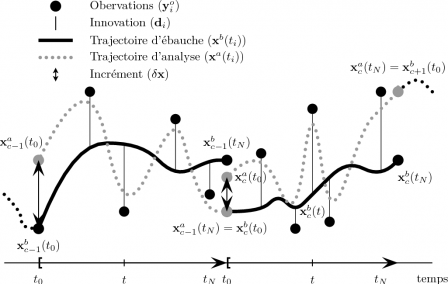
Fig. 4DVar : Illustration de la procédure pour cycler le 4D-Var incrémental. Pour chaque cycle \[c\], le modèle d'évolution est intégré de \[t_0\] à \[t_N\] à partir de l'état initial d'ébauche \[\mathbf{x}^b_c(t_0)\] (courbe noir pleine) et le vecteur d'innovation \[\mathbf{d}_i\] est calculé pour les différentes observations \[\mathbf{y}^o_i\] avec \[i=1,\cdots,N\] (ligne fine verticale). L'analyse est effectuée à l'instant \[t_0\] en ramenant les innovations à l'instant \[t_0\] à l'aide du modèle adjoint. Après la minimisation, un incrément est obtenu qui est rajouté à l'état de l'ébauche initial pour obtenir l'état analysé \[\mathbf{x}^a_c(t_0)=\mathbf{x}^b_c(t_0)+\delta\mathbf{x}^a\]. Cet état analysé tient compte de la dynamique du modèle de sorte que la trajectoire analysée (courbe grise pointillée) minimise au mieux l'écart aux observations tout au long du cycle d'assimilation (de \[t_0\] à \[t_N\]). L'état analysé \[\mathbf{x}^a_c(t_N)\] est ensuite utilisé comme état initial d'ébauche pour le cycle suivant.
Prise en compte des non-linéarités
A chaque itération de la minimisation, le terme de la fonction coût lié aux observations \[J^o(\delta\mathbf{x})\] est calculé en propageant l'incrément \[\delta\mathbf{x}\] dans le temps avec le modèle linéaire-tangent \[\mathbf{M}\]. Le calcul du gradient de la fonction coût, notamment de la partie relative aux observations \[\nabla J^o(\delta\mathbf{x})\], nécessite l'intégration de l'adjoint du modèle linéaire-tangent \[\mathbf{M}^T\] sur la fenêtre d'assimilation. A la fin de la minimisation, l'incrément d'analyse est ajouté à l'ébauche \[\mathbf{x}^b\] (Eq. (059}). L'état analysé à l'instant initial de la fenêtre d'assimilation \[\mathbf{x}^a\] est ensuite propagé par le modèle non-linéaire \[M\] jusqu'à la fin de la fenêtre permettant d'obtenir une trajectoire analysée \[\mathbf{x}^a(t_i)\]. En pratique, il est possible de prendre en compte les faibles non-linéarités des opérateurs \[H\] et \[M\] en mettant à jour la trajectoire de référence au cours de la minimisation. Ces mises à jours sont aussi appelée boucles externes. Le modèle linéaire est relinéarisé au voisinage du nouvel état de référence à chaque boucle externe et la fonction coût est ensuite minimisée par une série de boucles internes. Cette méthode permet de conserver la fonction coût quadratique tout en tenant compte, jusqu'à un certain point, des non-linéarités du système.
Commentaires
Bravo pour ce cours.
J'ai néanmoins un problème car les formules en Latex ne s'affiche pas correctement sur mon browser.
Auriez-vous une solution ?
Merci