Méthode d'assimilation - 3DVar
Par jOas le jeudi, novembre 15 2007, 23:51 - Assimilation - Lien permanent
3D-Var
La méthode d'assimilation variationnelle tri-dimensionnelle, notée 3D-Var pour "3Dimensional VARiational assimilation", consiste à chercher l'état le plus vraisemblable à partir des connaissances disponibles sur les lois de probabilités des erreurs d'observation et d'ébauche.
Comme sont nom l'indique clairement, le 3D-Var traite de problèmes tri-dimensionels. Par abus de langage, cette appellation est aussi utilisée pour des problèmes à une ou deux dimensions afin d'éviter les risques de confusions avec l'extension temporelle de cette méthode. En effet, sur un problème bi-dimensionnel, le 3D-Var s'appellerait 2D-Var, tandis que le 4D-Var se nommerait 3D-Var. Ce qui serait particulièrement ambigu. De ce fait, tous les problèmes ne prenant pas en compte l'aspect temporel sont appelés 3D-Var.
Comme pour le filtre de Kalman, le 3D-Var consiste à minimiser la distance au sens des moindres carrés entre l'état estimé et les différentes sources d'informations telles que la prévision précédente et les observations. Le nouvel état analysé est, en général, utilisé comme point de départ de la prévision suivante.
En reprenant les Eqs. (023) à (029), il est possible d'écrire la fonction coût
\[ J(\mathbf{x}) = \frac{1}{2}(\mathbf{x}-\mathbf{x}^b)^T\mathbf{B}^{-1}(\mathbf{x}-\mathbf{x}^b)+\frac{1}{2}(\mathbf{y}^o-H\mathbf{x})^T\mathbf{R}^{-1}(\mathbf{y}^o-H\mathbf{x})\],
En général, \[\mathbf{x}^b\] est issu de l'intégration par le modèle d'évolution de l'état analysé à l'étape précédente. L'équilibre entre le terme d'écart aux observations \[J^o\] et celui de l'ébauche \[J^b\] est effectué grâce aux inverses des matrices de covariances d'erreur d'observation et d'ébauche. C'est-à-dire grâce à la confiance portée dans les observations et l'ébauche.
La minimisation se fait à l'aide du gradient égale à
Comme montré dans la section sur le BLUE, si l'opérateur d'observation est linéaire (\[H=\mathbf{H}\]), le 3D-Var est alors équivalent au BLUE à l'optimalité, et donc aussi à l'interpolation optimale (Lorenc, 1986).
3D-Var classique
Dans un cadre théorique, il est possible d'imaginer des observations réparties régulièrement dans le temps. il est alors possible d'effectuer une analyse à chaque pas de temps où celles-ci sont présentes. En pratique, les observations sont diverses et très inégalement réparties. Afin de ne ma multiplier les phases d'analyse, une fenêtre temporelle de taille arbitraire est définie sur laquelle une analyse est effectuée. Dans le 3D-Var classique, toutes les observations sont regroupées (moyennées) à l'instant où est effectuée l'assimilation (Fig. 3DVar1). Dans ce cas, la méthode ne tient absolument pas compte de l'origine temporelle des observations hormis qu'elles doivent être incluses dans cette fenêtre temporelle. En faisant cette approximation, l'Eq. (045) s'écrit alors
\[ J^b(\mathbf{x}) = \frac{1}{2}(\mathbf{x}-\mathbf{x}^b)^T\mathbf{B}^{-1}(\mathbf{x}-\mathbf{x}^b)\],
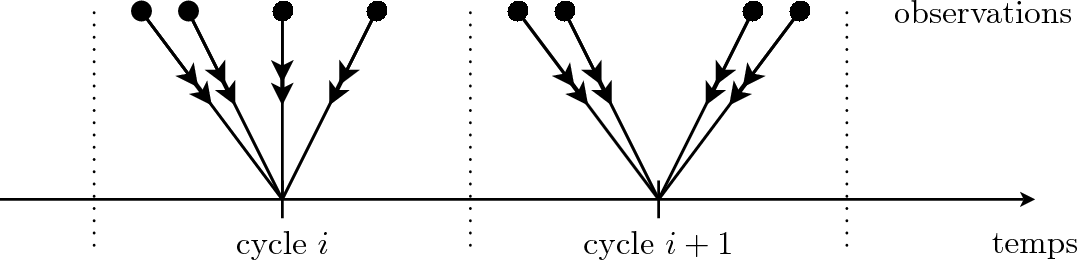
Fig. 3DVar1 : Répartition des observations dans un 3D-Var classique.
3D-Var FGAT
Le 3D-Var FGAT (First Guess at Appropriate Time) est un 3D-Var pour lequel les observations sont utilisées en tenant compte de l'instant de leurs mesures (Fig. 3DVar2). C'est-à-dire que chaque observation est comparée à l'état du modèle au pas de temps le plus proche. Néanmoins, la correction se fait toujours à un instant donné de la fenêtre (typiquement au début ou au milieu). L'équation (045} peut alors s'écrire
où \[\mathbf{y}_i\] représente les \[N\] observations de la fenêtre d'assimilation aux instants \[t_i\] et \[\mathbf{x}(t_i)\] représente l'état du modèle aux instants \[t_i\].
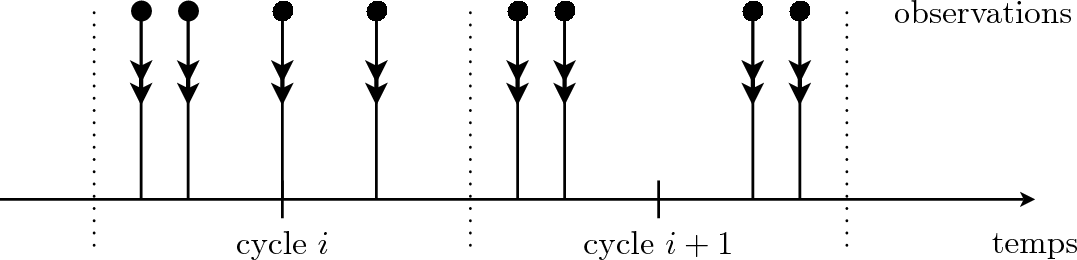
Fig. 3DVar2 : Répartition des observations dans un 3D-Var FGAT.
L'avantage du 3D-Var FGAT sur le 3D-Var classique est qu'il prend réellement en compte l'instant de mesure des observations. De plus, il est très similaire au 4D-Var présenté dans la suite.
3D-Var incrémental
Il est possible d'écrire le 3D-Var de manière incrémentale. L'intérêt de cette formulation sera discutée dans la section 4DVar où il apparaîtra clairement. Cette formulation consiste à considérer comme contrôle l'écart entre l'état du système et l'ébauche, et non plus l'état du système. L'introduction de l'approche incrémentale en météorologie a été motivée par la réduction de coût qu'elle propose en 4D-Var. Soit
\[\delta\mathbf{x} = \mathbf{x} - \mathbf{x}^b \].
La fonction coût devient alors
où \[\mathbf{d}\] est le vecteur d'innovation \[\mathbf{y}-H\mathbf{x}^b\].
La formulation 3D-Var FGAT (Eqs. (048a} et (048b}) prend alors la forme suivante :
\[ J^b(\delta\mathbf{x}) = \frac{1}{2}\delta\mathbf{x}^T\mathbf{B}^{-1}\delta\mathbf{x}\],
avec \[\mathbf{d}_i=\mathbf{y}^o_i - H\mathbf{x}(t_i)\].
Une illustration schématique (Fig. 3DVar3) du 3D-Var FGAT incrémental permet de comprendre simplement son utilisation. Il apparaît ainsi clairement que chaque analyse introduit un "choc" dans le modèle au moment de son introduction. Pour éviter cet inconvénient, il est possible d'utiliser une technique nommée IAU (Incremental Analysis Updating) et introduite par Bloom etal. (1996) qui consiste à répartir l'incrément d'analyse sur toute le cycle d'assimilation comme s'il s'agissait d'un forçage (Fig. 3DVar4).
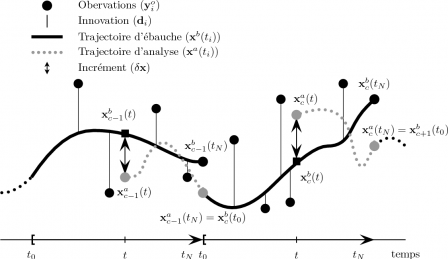
Fig. 3DVar3 : Illustration de la procédure pour cycler le 3D-Var FGAT incrémental. Pour chaque cycle \[c\], le modèle d'évolution est intégré de \[t_0\] à \[t_N\] à partir de l'état initial d'ébauche \[\mathbf{x}^b_c(t_0)\] (courbe noir pleine) et le vecteur d'innovation \[\mathbf{d}_i\] est calculé pour les différentes observations \[\mathbf{y}^o_i\] avec \[i=1,\cdots,N\] (ligne fine verticale). L'analyse est effectuée à l'instant \[t\] compris entre \[t_0\] et \[t_N\]. Après l'analyse, un incrément est obtenu et est rajouté à l'état d'ébauche \[\mathbf{x}^b_c(t)\] permettant d'obtenir l'état analysé \[\mathbf{x}^a_c(t)\]. L'état analysé est ensuite propagé jusqu'à le fin du cycle \[c\] (courbe grise pointillée). Cet état analysé \[\mathbf{x}^a_c(t_N)\] est ensuite utilisé comme état initial d'ébauche pour le cycle suivant.
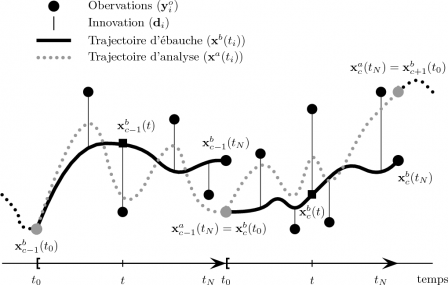
Illustration de la procédure pour cycler le 3D-Var FGAT incrémental avec IAU. Pour chaque cycle \[c\], le modèle d'évolution est intégré de \[t_0\] à \[t_N\] à partir de l'état initial d'ébauche \[\mathbf{x}^b_c(t_0)\] (courbe noir pleine) et le vecteur d'innovation \[\mathbf{d}_i\] est calculé pour les différentes observations \[\mathbf{y}^o_i\] avec \[i=1,\cdots,N\] (ligne fine verticale). L'analyse est effectuée à l'instant \[t\] compris entre \[t_0\] et \[t_N\]. Après l'analyse, un incrément est obtenu qui est rajouté comme un forçage lors de l'intégration du modèle d'évolution de \[t_0\] à \[t_N\] à partir de l'état initial d'ébauche \[\mathbf{x}^b_c(t_0)\] (courbe grise pointillée). Cet état analysé \[\mathbf{x}^a_c(t_N)\] est ensuite utilisé comme état initial d'ébauche pour le cycle suivant.