L'interpolation optimale (Gandin, 1963 ; Lorenc, 1981 ou Daley, 1991), notée OI, est une simplification algébrique du BLUE présenté précédemment. L'équation (009) est décomposée en un système d'équations résolvant cette équation pour chaque variable du modèle. L'hypothèse fondamentale de cette méthode est que pour chaque variable du modèle en chaque point de grille, un nombre réduit d'observations est pris prend en compte pour effectuer l'analyse. L'approximation vient donc de la technique de sélection d'une liste de données \[p_v\] utiles pour l'analyse de chaque variable \[\mathbf{x}_v\] en chaque point de grille. Le calcul de \[\mathbf{K}\] se fait ligne par ligne en n'utilisant qu'un nombre réduit d'observations voisines de chaque point de grille (Fig. 4).
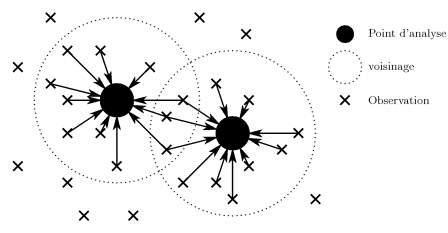
Fig. 4 : Représentation schématique de la sélection des observations au voisinage de deux points. Les analyses en ces deux points n'utilisent pas les mêmes observations bien qu'ils soient proches. Les champs analysé n'est donc généralement pas continu. De plus, le coût de l'analyse augmente avec la taille du voisinage utilisé.
Chose promise, chose due. Alors, voici une vision générale de ce qui occupe les plus longues de mes heures : l'assimilation de données.