Modèle de covariance d'erreur - Estimation des erreurs
Par jOas le vendredi, novembre 16 2007, 01:15 - Assimilation - Lien permanent
Il est difficile d'estimer les erreurs car elles ne sont jamais observées directement. En effet, l'état vrai n'étant pas accessible, il est impossible d'obtenir des échantillons des erreurs d'ébauche et d'observation. Les données statistiques sont donc difficilement disponibles et très largement insuffisantes pour déterminer tous les éléments. Par ailleurs, les matrices de covariances d'erreur sont très grandes. Pour ces deux raisons, elles doivent être simplifiées et modélisées. De tailles réduites, ces matrices sont manipulables informatiquement parlant et nécessitent moins de d'informations statistiques pour les décrire.
La modélisation des covariances d'erreur est donc un problème difficile et il est nécessaire de faire des hypothèses d'homogénéités. La meilleure source d'information est clairement l'étude de l'innovation (\[\mathbf{d}=\mathbf{y}-H\mathbf{x}^b\]) et peut être utilisée de plusieurs manières différentes. D'autres informations peuvent être obtenues à partir du vecteur d'erreur d'analyse (\[\mathbf{y}-H\mathbf{x}^a\]) ou à partir de la valeur de la fonction coût pour les méthodes variationnelles. D'autres méthodes permettent d'estimer les covariances d'erreur d'ébauche avec des quantités dont les statistiques d'erreur sont équivalentes à celle de l'erreur d'ébauche. Parmi ce type de techniques, la méthode NMC est très connue mais ces bases théoriques sont friables. Une autre possibilité est d'utiliser une méthode d'ensemble de la même manière que pour le filtre de Kalman éponyme. Cette méthode est néanmoins applicable quelque soit la méthode d'assimilation utilisée.
Méthode basée sur l'innovation
Cette méthode a été introduite en météorologie à la fin de années 80 (Hollingworth et Lönnberg, 1986). Elle est basée sur l'utilisation de l'innovation (\[\mathbf{d}=\mathbf{y}^o-H\mathbf{x}^b\]) d'un réseau d'observations suffisamment grand et dense tel qu'il puisse fournir des informations sur les différentes échelles présentes dans la physique du système. Cette méthode permet d'obtenir des statistiques moyennes permettant de construire des matrices de covariances d'erreur statiques. Deux hypothèses importantes sont émises : les erreurs d'ébauches sont indépendantes des erreurs d'observation et les erreurs d'observation ne sont pas corrélées spatialement. Le principe est ensuite assez simple (Fig. innovation)). Il suffit de construire un histogramme représentant les covariances de du vecteur d'innovation en fonction de la distance de séparation. Pour une séparation nulle, l'histogramme fournit une information moyenne sur les variances d'erreurs d'ébauche et d'observation. Pour une distance non-nulle, l'histogramme ne fournit plus qu'une information moyenne sur les corrélations d'erreur d'ébauche.
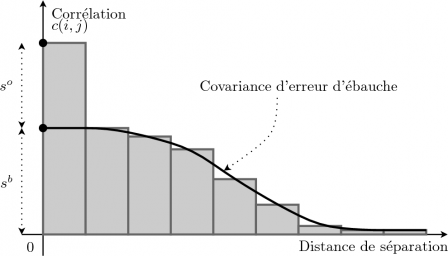
Fig. innovation : Représentation de la méthode basée sur l'innovation. Les statistiques de covariances de l'innovation (\[\mathbf{y}^o-H\mathbf{x}^b\]) d'un système d'assimilation sont rangées dans un histogramme en fonction de la distance séparant les deux points. L'histogramme à l'origine permet d'estimer les variances d'ébauche et d'observation moyennes.
Soit deux points d'observation \[i\] et \[j\], la covariance d'innovation \[c(i,j)\] s'écrit
\[ c(i,j)=E\left[(\mathbf{y}^o_i-\mathbf{H}_i\mathbf{x}^b)(\mathbf{y}^o_j-\mathbf{H}_j\mathbf{x}^b)^T\right]\]
\[c(i,j)=E\left[\left((\mathbf{y}^o_i-\mathbf{H}_i\mathbf{x}^t)+(\mathbf{H}_i\mathbf{x}^t-\mathbf{H}_i\mathbf{x}^b)\right)\left((\mathbf{y}^o_j-\mathbf{H}_j\mathbf{x}^t)+(\mathbf{H}_j\mathbf{x}^t-\mathbf{H}_j\mathbf{x}^b)\right)^R\right]\]
\[c(i,j)=E\left[(\mathbf{y}^o_i-\mathbf{H}_i\mathbf{x}^t)(\mathbf{y}^o_j-\mathbf{H}_j\mathbf{x}^t)^T\right]+ \mathbf{H}_i E\left[(\mathbf{x}^t-\mathbf{x}^b)(\mathbf{x}^t-\mathbf{x}^b)^T\right]\mathbf{H}_j^T\]
\[ +E\left[(\mathbf{y}^o_i-\mathbf{H}_i\mathbf{x}^t)(\mathbf{x}^t-\mathbf{x}^b)^T\right]\mathbf{H}_j^T+ \mathbf{H}_iE\left[\mathbf{x}^t-\mathbf{x}^b)(\mathbf{y}^o_j-\mathbf{H}_j\mathbf{x}^t)^T\right]\]
En utilisant l'hypothèse que l'erreur d'ébauche n'est pas corrélée à l'erreur d'observation, l'Eq. (067) ne conserve que deux termes : le premier est la covariance d'erreur d'observation entre les points \[i\] et \[j\] ; le second est la matrice de covariances d'erreur d'ébauche interpolée (si l'opérateur d'observation n'agit qu'en tant qu'opérateur d'interpolation) en ces points. Ceci en supposant que ces deux termes sont homogènes sur l'ensemble des observations.
Si les points \[i\] et \[j\] sont identiques (\[i=j\]), alors la corrélation du vecteur d'innovation au point \[i\] est la somme des variances d'erreurs d'ébauche et d'observation (\[c(i,j)=s^o_i+s^b_i\]). Si les points \[i\] et \[j\] sont différents (\[i\neq j\]) et que l'erreur d'observation n'est pas corrélée spatialement, alors la corrélation du vecteur d'innovation entre les points \[i\] et \[j\] est la covariance d'erreur d'ébauche entre ces points (\[c(i,j)=\mathbf{H}_i\mathbf{B}\mathbf{H}_j^T\]). A noter que la décorrélation spatiale d'erreur d'observation est fondamentale, car seule cette hypothèse permet de séparer l'information provenant de la matrice de covariances d'erreur d'observation \[\mathbf{R}\] et d'ébauche \[\mathbf{B}\].
A partir de ces hypothèses, si les points \[i\] et \[j\] sont très proches l'un de l'autre sans jamais être égaux, alors la corrélation du vecteur d'innovation entre les point \[i\] et \[j\] tend vers la variance d'erreur d'ébauche au point \[i\] (\[\lim_{i\to j}c(i,j)=s^b_i\]). En prolongeant la courbe formée par la corrélation du vecteur d'innovation vers une séparation nulle, il est donc possible d'obtenir la variance d'erreur d'ébauche. La variance d'erreur d'observation est alors la différence entre la corrélation du vecteur d'innovation pour une séparation nulle et la variance d'erreur d'ébauche obtenue (\[s^o_i=c(i,j)-s^b_i\]). Il est aussi possible d'obtenir les corrélations d'erreur d'ébauche en fonction de la distance de séparation en prenant le rapport de la corrélation du vecteur d'innovation sur la variance d'erreur d'ébauche (\[c(i,j)/s^b_i\]). Ce résultat n'est possible que si les variances d'erreur d'ébauche sont homogènes sur tout le jeu d'observations.
Si les covariances d'erreur d'ébauche ne tendent pas vers zéro pour unegrande distance de séparation, c'est le signe de la présence d'un biais dans l'ébauche et/ou les observations. Dans ce cas, cette méthode ne fonctionnera pas correctement.
La méthode basée sur l'innovation est la seule méthode directe permettant de diagnostiquer les statistiques d'erreur. Cependant, elle ne fournit des informations que dans l'espace des observations et donc que dans les régions observées. Pour obtenir de bons résultats, il faut un réseau d'observations uniforme et pas trop dense pour ne pas biaiser les statistiques. Cette méthode n'est donc pas toujours très pratique pour spécifier les statistiques des erreurs. De plus, elle ne fournit que des valeurs moyennes ne permettant que de construire des matrices de covariances d'erreur statiques.
Méthode NMC
La méthode NMC (Parrish et Derber, 1992) est ou a été utilisée dans de nombreux centres de prévision météorologique. Elle permet de construire de construire une matrice de covariances d'erreur d'ébauche statique. L'idée est de calculer des différences entre des prévisions valides au même instant mais de durées différentes. A partir de ces différences, il est possible de d'obtenir des statistiques qui peuvent être liées à la matrice de covariances d'erreur d'ébauche \[\mathbf{B}\]. A partir d'un système d'assimilation séquentielle, il est très facile de mettre cette méthode en oeuvre. A la fenêtre d'assimilation démarrant à l'instant \[t_{i-1}\], une prévision d'une durée de deux cycles d'assimilation est effectuée (de \[t_{i-1}\] à \[t_{i+1}\]). A partir du même état à l'instant \[t_{i-1}\], un cycle d'assimilation est effectué et permettent d'obtenir un état à l'instant \[t_i\] à partir duquel une prévision est effectuée de d'une durée d'un cycle (de \[t_i\] à \[t_{i+1}\]). Ces deux prévisions sont donc valides au même instant \[t_{i+1}\]. Il est possible d'envisager ces deux prévisions comme des prévisions d'une durée d'un seul cycle d'assimilation mais dont les conditions initiales à \[t_i\] varient. Ces différences de conditions initiales reflètent l'impact de l'assimilation. En calculant les différences entre ces deux prévisions et en reproduisant ces expériences suffisamment de fois, il est alors possible de calculer des statistiques sur ces différences. Le principe de la méthode NMC est illustré par la Fig. NMC.
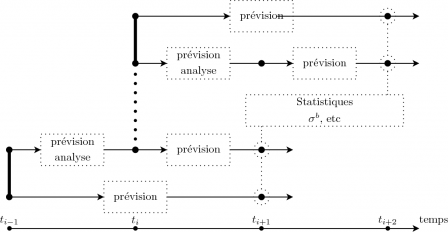
Fig. NMC : Méthode NMC. Une prévision démarre à \[t_{i-1}\] et dure jusqu'à \[t_{i+1}\]. Au même instant, une analyse est effectuée entre \[t_{i-1}\] et \[t_i\]. Suite à l'analyse, une prévision est effectuée jusqu'à l'instant \[t_{i+1}\]. Les différences entre les deux prévisions à l'instant \[t_{i+1}\] sont calculées. Ce processus est répété à partir de l'instant \[t_i\] et ainsi de suite. Toutes les différences permettent alors d'estimer la matrice de covariances d'erreur d'ébauche \[\mathbf{B}\].
Comme le met en évidence Berre \etal (2006), l'erreur d'analyse s'écrit
\[ {\epsilon}^a_{i}={\epsilon}^b_{i}+\mathbf{K}({\epsilon}^o_{i}+H{\epsilon}^b_{i})\],
\[ {\epsilon}^a_{i}=(\mathbf{I}-\mathbf{K} H){\epsilon}^b_{i}+\mathbf{K}{\epsilon}^o_{i}\],
et la différence entre les conditions initiales des deux prévisions à l'instant \[t_i\] s'écrit
\[ \delta \mathbf{x}^a_i=\mathbf{x}^a_i-\mathbf{x}^b_i\],
\[ \delta \mathbf{x}^a_i=\mathbf{K}({\epsilon}^o_i-H{\epsilon}^b_i)\],
\[ \delta \mathbf{x}^a_i=-\mathbf{K} H{\epsilon}^b_i+\mathbf{K}{\epsilon}^o_i\].
Les matrices \[\mathbf{I}-\mathbf{K} H\] et \[\mathbf{K}\] représentent les poids des erreurs d'ébauche et d'observation dans l'équation d'analyse. Dans la méthode NMC, le poids de l'erreur d'ébauche est approximé par \[-\mathbf{K} H\]. Cette approximation est raisonnable si \[\mathbf{K} \sim \mathbf{I} / 2\] (Boutier, 1994). Ce cas de figure est décrit par un réseau d'observations très denses (\[H \sim \mathbf{I}\]) et des matrices de covariances d'erreur presque identiques (\[\mathbf{R} \sim H\mathbf{B} H^T \sim \mathbf{B}\]). La deuxième condition signifie que l'erreur d'observation possède la même intensité et les mêmes structures spatiales que l'erreur d'ébauche.
Cependant, dans les régions pauvres en observations ou avec des observations de piètre qualité, l'incrément d'analyse risque d'être faible tandis que l'erreur d'analyse sera grande.
De plus, l'erreur d'observation est généralement moins corrélée spatialement que l'erreur d'ébauche. Comme le montre Daley (1991, section 4.5), l'opérateur \[\mathbf{K} H\] agit comme un filtre passe-bas. Par conséquence, l'opérateur \[\mathbf{I}-\mathbf{K} H\] devrait agir comme un filtre passe-haut. Ce qui signifie que l'incrément d'analyse doit avoir un spectre plus large que l'erreur d'analyse. Les corrélations d'erreur d'analyse risquent donc d'être surestimées avec la méthode NMC.
La perturbation d'analyse à l'instant \[t_i\] est ensuite propagée par le modèle d'évolution jusqu'à \[t_{i+1}\]. Les différences entre les prévisions permettent donc d'estimer l'erreur d'ébauche à la condition que \[\mathbf{K} \sim \mathbf{I} / 2\].
La méthode NMC a de nombreux avantages. Elle permet d'obtenir des statistiques dans l'espace du modèle et donc pour toutes les variables du modèle. De plus, elle est très bon marché. Cependant, elle ne représente pas parfaitement l'erreur d'ébauche car les hypothèses faites ne sont pas respectées. Ainsi, l'estimation de l'erreur d'ébauche est trop faible dans les régions peu ou mal observée.
Méthode d'ensemble
La méthode d'ensemble a d'abord été proposé par Evensen (Evensen, 1994) dans le cadre du filtre de Kalman d'ensemble. Néanmoins, cette méthode peut s'appliquer aux autres méthodes d'assimilation.
L'idée de cette méthode est de construire un ensemble composé d'une série de membres perturbés. Chacun des membres est analysé puis propagé de fenêtre d'assimilation en fenêtre d'assimilation. Ainsi, chaque membre est traité individuellement. Il est alors possible de calculer des différences entre ces membres à n'importe quel instant, puis d'obtenir des statistiques sur ces différences. La figure ens_algo permet d'illustrer l'algorithme.
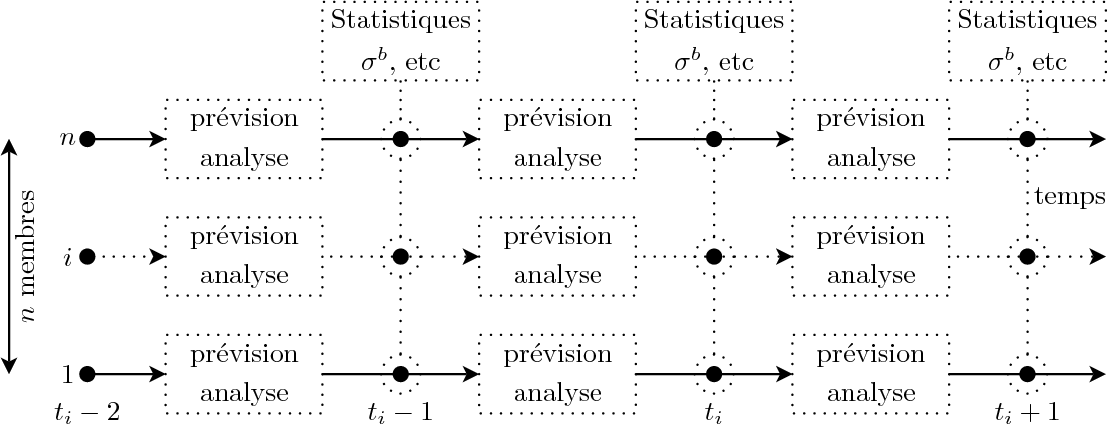
Fig. ens_algo : Méthode d'ensemble. Un ensemble est constitué de \[n\] membres perturbés qui analysés et propagés indépendamment. Après chaque cycle d'assimilation, les différences entre ces membres permettend d'obtenir des statistiques estimant la matrice de covariances d'erreur d'ébauche \[\mathbf{B}\].
Il existe un lien entre les statistiques obtenues avec les différences entre les membre et l'erreur d'ébauche. En effet, les perturbations ajoutées aux membres de l'ensemble évoluent de manière similaire à l'erreur du système d'assimilation. Ainsi, à condition de bien spécifier les perturbations, les statistiques obtenues avec les différences entre les membres sont une très bonne estimation de l'erreur d'ébauche.
Cependant, il est difficile de bien perturber les membres de l'ensemble, car les perturbations appliquées aux divers champs doivent être similaires aux covariances d'erreur de ces champs. Le problème de la connaissance de la matrice de covariances d'erreur d'ébauche est ainsi déplacé vers la connaissance des matrices de covariances d'erreur des champs perturbés. Néanmoins, ces champs à perturber peuvent être mieux connus ou leurs covariances d'erreur plus accessible.
La méthode d'ensemble est donc une méthode complexe et coûteuse. Elle a cependant des attraits non-négligeables. Elle permet d'estimer réellement les erreurs d'ébauche de toutes les variables du modèle au cours du temps. Il est ainsi possible d'obtenir une matrice de covariance d'erreur d'ébauche \[\mathbf{B}\] dynamique. Cette méthode a cependant un défaut important. Si le système d'analyse est bruité, les statistiques le seront aussi et amplifieront le bruit du système d'analyse. Il est donc nécessaire d'être attentif aux risques de rétroaction.