Interpolation statistiques - L'exemple du naufragé
Par jOas le jeudi, novembre 15 2007, 12:42 - Assimilation - Lien permanent
Pour illustrer les différents concepts abordés, un exemple sera très utile. Supposons qu'à la suite d'une tempête, un marin naviguant en suivant la ligne de côtes, s'échoue sur des récifs. Le bateau étant bien équipé, il relève sa dernière position sur le GPS et monte dans le canot de sauvetage. Malheureusement, ce canot est dépourvu de rames. Les vagues et le vent l'emportent donc loin de son navire échoué. Définissons un référentiel de tel sorte que l'axe x soit parallèle à la côte et l'axe y lui soit perpendiculaire. La position du navire échoué dans ce référentiel est défini comme le point de référence de coordonnées (0,0). La position du canot de sauvetage est donc connu à l'instant \[ t_0=0 \]. Un peu plus tard, à l'instant t, le naufragé estime au jugé la distance qui le sépare de la côte. Le naufragé sait que son estimation est empreinte d'une erreur et il estime la variance de cette erreur \[s^o\]. Il se rappelle, par ailleurs, la position de l'épave et sait que le canot de sauvetage a dérivé malgré l'absence de courants marins prédominants dans cette région. Il suppose donc que la probabilité qu'il se trouve maintenant à la position \[(u^b,v^b)\] suit une loi normale de variance \[s^b\] qui dépend linéairement du temps écoulé. Après réflexion, il estime aussi que le processus de mesure au jugé n'est pas corrélé à celui de la dérive du canot. Il résume donc sa situation en faisant un schéma (Fig. 3).
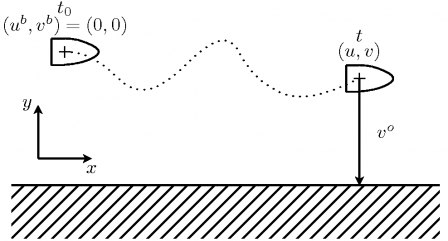
Fig. 3 : La géométrie de la situation du naufragé.
Définition des variables
Dans cette situation, le naufragé ne perdant pas son sang-froid, définit les variables lui permettant de résoudre son problème. Il commence par construire un vecteur d'état \[ \mathbf{x}=(u,v)^T\] et le vecteur d'observation \[\mathbf{y}^o=v^o\]. Il n'a, en effet, aucune possibilité de mesurer sa position le long de la côte. Dans ce cadre, il peut définir son opérateur d'observation simplement par \[\mathbf{H}=(0,1)\]. Comme il a estimé la variance de l'erreur de sa mesure, il construit la matrice de covariance d'erreur sur l'observation telle que \[\mathbf{R}=(s^o)\]. Finalement, il construit sa matrice de covariance d'erreur d'ébauche en utilisant son hypothèse sur une dérive suivant une loi normale et il obtient :
\[ \mathbf{B} = \left( \begin{array}{cc} s^b & 0 \\ 0 & s^b \end{array} \right)\].
Analyse optimale
Comme ce navigateur lisait régulièrement des ouvrages d'assimilation de données, il sait qu'il peut faire une estimation de sa nouvelle position en utilisant le BLUE. Il commence par écrire l'analyse de manière théorique \[\mathbf{x}^a=\mathbf{x}^b+\mathbf{K}(\mathbf{y}^o-\mathbf{H}\mathbf{x}^b) \] puis l'applique à sa situation :
\[ \left( \begin{array}{c} u^a \\ v^a \ \end{array} \right) = \left( \begin{array}{c} 0\\0 \end{array} \right) +\mathbf{K} \left( v^o - (0,1) \left( \begin{array}{c} 0\\0 \end{array} \right) \right) = \left( \begin{array}{c} 0\\\mathbf{K} v^o \end{array} \right) \].
Connaissant l'Eq. (015), il sait que \[ \mathbf{K}^*=\mathbf{B}\mathbf{H}^T(\mathbf{R}+\mathbf{H}\mathbf{B}\mathbf{H}^T)^{-1} \]. Il calcule donc le gain optimal \[ \mathbf{K}^*\] :<\p>
\[ \mathbf{K}^* = s^b \left( \begin{array}{c} 0\\1 \end{array} \right) \left( s^o+(0,1)s^b \left( \begin{array}{c} 0\\1 \end{array} \right) \right)^{-1} \],
\[ \mathbf{K}^* = s^b \left( \begin{array}{c} 0\\1 \end{array} \right) \left( s^o+ s^b \right) \], \[ \mathbf{K}^* = \frac{s^b}{s^o+s^b} \left( \begin{array}{c} 0\\1 \end{array} \right) \].
Le malheureux naufragé peut alors estimer plus précisément sa position et en déduit que :
\[ \left( \begin{array}{c} u^a \\ v^a \ \end{array} \right) = \frac{s^b}{s^o+s^b} \left( \begin{array}{c} 0\\v^b \end{array} \right) \].
Il constate donc logiquement que n'ayant pas apporté d'information sur sa position le long de la côte, la meilleure estimation possible est de conserver sa position au moment du naufrage \[u^a=0\]. Il constate aussi que plus le temps s'écoule, plus l'erreur sur son ébauche \[ s^b\] grandit de sorte que la meilleure estimation de la distance le séparant de la côte tend vers son observation au jugé (\[\lim_{t \to \infty} v^a=v^o\]).
Erreur commise
De plus, notre naufragé connaît aussi la formule liant la matrice de covariance d'erreur d'analyse à celle d'ébauche (Eq. (017)) qui est \[ \mathbf{A}=(\mathbf{I}-\mathbf{K}\mathbf{H})\mathbf{B} \] et l'estime alors pour son cas :
\[ \mathbf{A}=\left( \begin{array}{cc} s^b & 0 \\ 0 & \frac{s^o s^b}{s^o+s^b} \end{array} \right)\].
Il lui apparaît alors encore plus clairement que son analyse ne permet pas d'augmenter sa connaissance sur sa position le long de la côte et que son incertitude est celle de sa dérive. Il apprend, par contre, que son analyse permet de réduire l'incertitude sur la distance le séparant de la côte d'un facteur \[ s^o/(s^o+s^b)\]. Ainsi, plus il sera capable d'obtenir une observation précise, plus il réduira l'erreur. En effet, comme le montre l'Eq. (020), en notant \[s^a\] la variance de l'erreur sur la coordonnée \[v\] après analyse, on obtient :
\[ \frac{1}{s^a}=\frac{1}{s^o}+\frac{1}{s^b}\].
Il apparaît encore plus clairement que l'ajout d'une information augmente forcément la qualité de l'analyse. Et ceci, quelque soit la qualité de l'information.
Après ces différents résultats, le naufragé est bien avancé et décide d'utiliser son énergie à trouver une solution à son autre problème : regagner la terre ferme.