Méthode d'assimilation - Interpolation Optimale (OI)
Par jOas le jeudi, novembre 15 2007, 16:46 - Assimilation - Lien permanent
L'interpolation optimale (Gandin, 1963 ; Lorenc, 1981 ou Daley, 1991), notée OI, est une simplification algébrique du BLUE présenté précédemment. L'équation (009) est décomposée en un système d'équations résolvant cette équation pour chaque variable du modèle. L'hypothèse fondamentale de cette méthode est que pour chaque variable du modèle en chaque point de grille, un nombre réduit d'observations est pris prend en compte pour effectuer l'analyse. L'approximation vient donc de la technique de sélection d'une liste de données \[p_v\] utiles pour l'analyse de chaque variable \[\mathbf{x}_v\] en chaque point de grille. Le calcul de \[\mathbf{K}\] se fait ligne par ligne en n'utilisant qu'un nombre réduit d'observations voisines de chaque point de grille (Fig. 4).
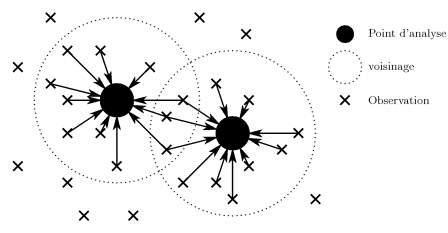
Fig. 4 : Représentation schématique de la sélection des observations au voisinage de deux points. Les analyses en ces deux points n'utilisent pas les mêmes observations bien qu'ils soient proches. Les champs analysé n'est donc généralement pas continu. De plus, le coût de l'analyse augmente avec la taille du voisinage utilisé.
La matrice de gain \[\mathbf{K}\] est construite par bloc et sa formulation se fait à un coût réduit :
où v représente les points au voisinage du point d'analyse variant de 1 à V et où :
La matrice \[\mathbf{P}_v\] de l'Eq. (031), de dimension, p x p définit quelles sont les observations au voisinage du point d'analyse qui seront utilisées pour le calcul de \[\mathbf{K}_v\]. Le calcul de \[\mathbf{K}\] se résume donc à l'inversion de V systèmes réduits de \[(p_v\times p_v)\] équations. La solution donnée par l'OI est optimale à l'instant de l'analyse sur chaque voisinage, mais est sous-optimale relativement à l'ensemble des observations (sur la période de mesure et sur l'ensemble du domaine de mesure).
Avantages : méthode simple et bon marché
L'OI présente l'avantage de s'implémenter aisément et de fournir une analyse à moindre coût par rapport à l'application exacte du BLUE, notamment pour le calcul de la matrice de gain \[\mathbf{K}\]. D'autre part, la matrice \[\mathbf{B}\] ne doit pas nécessairement être explicitée dans sa globalité. Elle peut être définie pour chaque variable par des fonctions empiriques d'autocorrélations constantes au cours du temps, des contraintes physiques du système telles que l'équilibre hydrostatique ou géostrophique en océanographie ou par des EOF (Empirical Orthogonal Function) univariées ou multivariées
Inconvénient : analyse bruitée
L'inconvénient majeur de cette méthode vient du choix des voisinages d'influence des observations en chaque point de grille qui produit une analyse bruitée (Cohn \etal, 1998). Ceci peut être aggravé par le choix de spécifications incompatibles des erreurs d'ébauche pour chaque variable du modèle.